Kugelvolumen herleitung integral

Kugel mit Loch reingebohrt - Volumen per. Willkommen zu diesem Sofatutor-Video, dass sich mit dem Kegelvolumen und der Herleitung der Formel befasst. Damit du das Video verstehst, brauchst du fundierte Vorkenntnisse über Reihen und. Video wird das Volumen einer Kugel berechnet.

Aber nicht der mathematische sondern der physikalische Weg. Aber ich wollte wissen ob ihr eine gute Seite kennt. Leiten Sie ebenso eine Formel für das Volumen des Kugelabschnittes (Kugelhaube) mit der Höhe h her!

Hinweis: Bei r = h liegt eine Halbkugel vor! Beliebte Inhalte auf Schulminator. So bestimmen Sie Oberfläche und Volumen einer Kugel. Archimedes, der Kreis und die Kugel Ungekürzte Fassung des Artikels von Markus Ruppert aus dem ML-Heft Nr.

Prinzip von Cavalieri Zwei Körper sind volumengleich, wenn sie folgende Bedingungen erfüllen: 1. Hi erstmal vielen Dank für die Antwort. Das heiˇt, die Berechnung des Fl ac henintegrals ub er Das heiˇt, die Berechnung des Fl ac henintegrals ub er ein Rechteck kann man sich wie folgt vorstellen (mittlere Formel). Die Oberkante stellt die Funktion f(x) dar. Spiegelbildlich entsteht dazu durch die Rotation die untere Begrenzungsli-nie, die man durch f(x) beschreiben k onnte.

Integrale existieren. Es wird überlegt, wie man die Kugel im Koordinatensystem positioniert und welche Funktion man benötigt, um sie als Rotationskörper um die x-Achse darzustellen. Diese Funktion wird dann in die Volumenformel für Rotationskörper eingesetzt und man bekommt die Volumenformel für Kugeln, die auch im Tafelwerk zu finden ist. Die Schüler leiten dabei selbst mit dem Material die Volumenformel für die Kugel her.

Die nachstehende ist wieder etwas schwieriger. Woher soll ich dann dies wissen? Kugelvolumen ( Herleitung über Doppelintegral). GFS zu dem Thema Mittelwerte von Funktionen. Soweit habe ich alles durchgearbeitet, mir fehlt nur eine vernünftige Erklärung zu der Herleitung der Formel.

Ich finde dazu wirklich nichts. Jedoch hab ich keine Ahnung wie man auf genau diese Formel kommt, also der Herleitung, und brauche daher einfach ein bisschen Hilfe von jemandem, der sich in diesem Gebiet auskennt. Im Mathe-Forum OnlineMathe. Fragen zur Mathematik beantwortet. Ich komme bei diesem Beispiel auf 268.

Warumwohl stimmt meine Lösung auch? Kugel Formel berechnen: Kugel Volumen , Kugel Oberfläche. Eine Kugel hat einen Mittelpunkt M von dem aus alle Punkte auf der Oberfläche gleich weit entfernt sind.

Die Entfernung ist der Radius r. Die Kugel ist ein Rotationskörper. Sie entsteht, wenn ein Halbkreis um seinen Durchmesser rotiert. Der Mittelpunkt des Kreises ist auch der.

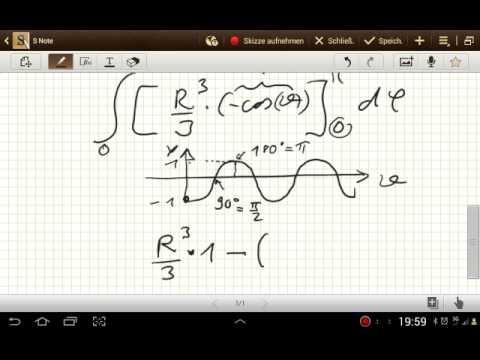
Bei einer Halbkugel wird der Radius (Höhe) in n Teile geteilt und daraufhin in Scheiben zerschnitten. Die Volumina der Scheiben lassen sich berechnen. Es entsteht zum Beispiel, wenn man eine Funktion f(x) um die x-Achse rotieren lässt.