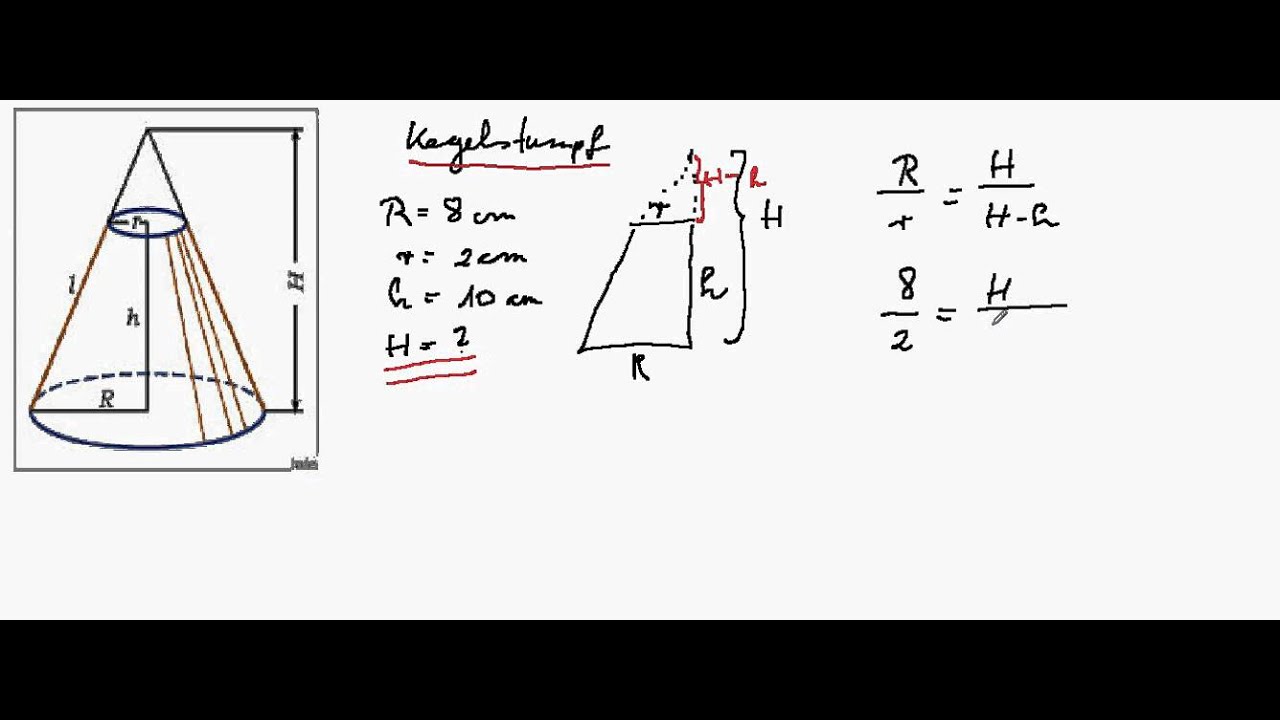
Die Grundfläche ist der größere Kreis, die Deckfläche der kleinere. Die Mantellinie ist die kürzeste Verbindung der beiden Kreisflächen, die Mantelfläche ist die Oberfläche ohne die beiden Kreisflächen. Einfach zwei Werte eingeben, alle anderen Ergebnisse werden automatisch berechnet. Der Kegel wird in 3D dargestellt und verändert sich interaktiv mit den Eingaben. Berechnet hier einen Kegel online.
Die Höhe der Seitenfläche des kleinen Kegels lässt sich nicht berechnen , da ich um die Seitenfläche des Kegelstumpfes berechnen zu können und später die Gesamthöhe der Seitenfläche abziehen zu müssen, damit ich die Differenz kenne wissen muss welche Maße der Radius der zweiten Grundfläche hat. Nun stelle ich mir die Frage wie ich die Formel umstellen kann, könnte mir eventuell jemand helfen ? Diese müsste ich dann vom. Vielleicht auch nur ein Tipp etc. Lösung schreiben, dass bringt mir wirklich nicht viel.
Ich stelle einmal eine Proberechnung ein. Kegelstumpf ist in der Geometrie die Bezeichnung für einen speziellen Rotationskörper. Verständliche Videos und Übungen.
Interaktiv und mit Spaß lernen. Trage die Länge der Seitenkante ein (Satz des Pythagoras). Die Länge der Seitenkante beträgt cm. Das ist schon klar, dass das Volumen des Kegelstumpfes dem Volumen des Kegels minus dem Volumen des Ergänzungskegels entspricht!
Das Problem ist: Wie kommt man von. Pyramidenstumpf - Rechner. Bei Zeichnungsangaben ist zwischen den Begriffen Neigung und Verjüngung zu unterscheiden. Kegelige Formen stellen in der Bemaßungstechnik einen Spezialfall dar.
Mathe: Kegelstumpf berechnen für Schablone Hallo zusammen, ich möchte mir gerne eine Schablone eines Kegelstumpfmantels anfertigen. Die Formeln habe ich von dieser Seite. Jetzt kostenlos ausprobieren! Prüfe dein Wissen anschließend mit Arbeitsblättern und Übungen.
Das Volumen in Höhe von Liter scheint nicht richtig zu sein. Schon bei 1dm Höhe wäre es, grob geschätzt, mehr als 2Liter. Für mich sind das keine Durchmesser, sondern Teillängen, besser gesagt Radien. Folglich ist auch die Formel für den Kegelstumpf nicht benutzt worden.

Die Benutzung der Formel hätte den algebraischen Gleichungsteil erheblich verkompliziert. Genauso wäre der Term des Strahlensatzes deutlich umständlicher geworden, wenn man z. Für den hohlen Kegelstumpf gilt nun Im Falle des Hohlzylinders konnte man einen derartigen Ausdruck faktorisieren Mit einem neuen Polynom Q, d. Differenz der Polynome V erhalten, die die Volumina definieren. Mathepower löst auch deine Mathematik - Hausaufgaben.
Im vorliegenden Fall des Kegelstumpfs sehe ich jedoch nicht, wie eine derartige Faktorisierung möglich sein soll.
Keine Kommentare:
Kommentar veröffentlichen
Hinweis: Nur ein Mitglied dieses Blogs kann Kommentare posten.